Skip to main content
2025 PharmSci 360 Main banner
Icon Legend
This session is not in your schedule.
This session is in your schedule. Click again to remove it.

Preclinical, Clinical, and Translational Sciences

Effectiveness of Droplet Digital PCR (ddPCR) and Hybridization (ECLIA) for Bioanalysis and Biodistribution of Gene Therapy Products

(M1530-05-33) Effectiveness of Droplet Digital PCR (ddPCR) and Hybridization (ECLIA) for Bioanalysis and Biodistribution of Gene Therapy Products

Monday, November 10, 2025
3:30 PM - 4:30 PM CT
Purpose: As gene therapy continues to gain traction, the need for precise and accurate measurement of nucleotide-based test compounds in vivo is growing significantly. These molecules vary widely in size and chemistry, including but not limited to mRNA, short guide DNA, microRNA, and siRNA. Due to their inherent properties, even a minimal dose can result in substantial functional alterations by suppressing, modulating or restoring gene expression. Therefore, sensitive methodologies are essential to characterize the pharmacokinetics and biodistribution properties of gene therapy products for safety assessment purposes. In this study, we evaluated the effectiveness of Droplet Digital PCR (ddPCR) and Hybridization Electrochemiluminescence Immunoassay (ECLIA) for bioanalysis and biodistribution of nucleotide-based targets. We used genomic DNA as a representative of long and DNA-based molecules and microRNA as a representative of small RNA molecules, thus covering the complete spectrum of nucleotide-based molecules in both length and type (RNA vs DNA), as used in gene therapy.

Methods: Genomic DNA (gDNA) was used as a surrogate for long DNA molecules and microRNA 122 (miR-122) as a representative short RNA molecule. Because ddPCR requires a minimum length of 70 bp, we extended the microRNA template using hybridization and ligation steps. The genomic DNA was directly quantified. Additionally, we used a hybridization Electrochemiluminescence Immunoassay (ECLIA) to detect miR-122, achieved through hybridizing to a dual-labeled probe followed by digestion and detection. Both gDNA and miR-122 were spiked and diluted into various matrices, including plasma and several homogenized organs, before analysis by ddPCR or Hybridization ECLIA.

Results: Using gDNA, the ddPCR platform achieved remarkable sensitivity, with a lower limit of quantification (LLOQ) in the low femtomolar (fM) range (Figure 1), coupled with impressive precision (%CV) and accuracy (%RE) in plasma. While ddPCR is ideally suited for quantifying target products longer than 70 bp, shorter molecules pose challenges. Therefore, to utilize this technology for smaller molecules such as microRNAs, the template must first be extended to accommodate the necessary elements for the amplification reaction. Using miR-122, we extended the template using the hybridization approach discussed above but the reproducibility of the ddPCR results were very poor (Figure 2). Given the proven robustness of ddPCR on longer DNA molecules, we concluded that the hybridization and ligation step was likely responsible for the lack of reproducibility observed. Recognizing the prevalence of microRNAs as gene therapy tools, we aimed to develop a hybridization-based Electrochemiluminescence Immunoassay (ECLIA) method specifically designed to detect shorter oligonucleotides. Using this technique, we were able to achieve high precision and accuracy across various matrices including organs with acceptable inter-assay precision and accuracy (Figure 3). While not as sensitive as ddPCR, Hybridization ECLIA demonstrated sensitivity within the lower end of the nanomolar (nM) range.

Conclusion: Our study demonstrates that ddPCR is a highly powerful platform for developing extremely sensitive bioanalytical and biodistribution assays for gene therapy products greater than 70 bp in length. For shorter oligonucleotides, such as microRNAs, siRNA molecules, or guide DNAs, Hybridization ECLIA provides an excellent alternative approach. Although not as sensitive as ddPCR, it still demonstrates acceptable lower limit of quantification (LLOQ) while maintaining a high level of precision and accuracy. Overall, our findings suggest that the length of gene therapy products is a critical factor in determining the optimal approach for bioanalysis and biodistribution in preclinical safety studies.

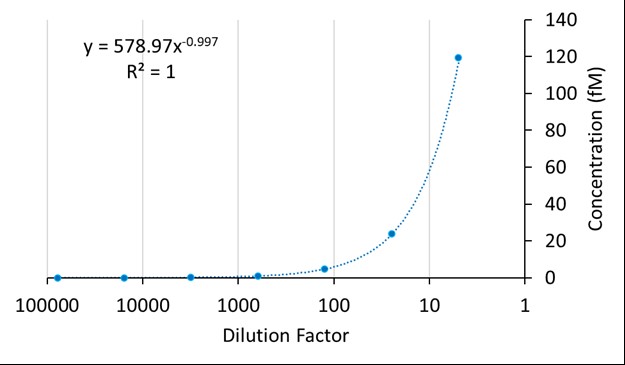Figure 1. ddPCR analysis is an extremely precise, accurate, and sensitive method for quantifying nucleic acid-based test items. Representative power regression curve (y = mx^b) of spiked DNA template in pooled Rat plasma with a limit of detection of ~0.01 fM nominal concentration.

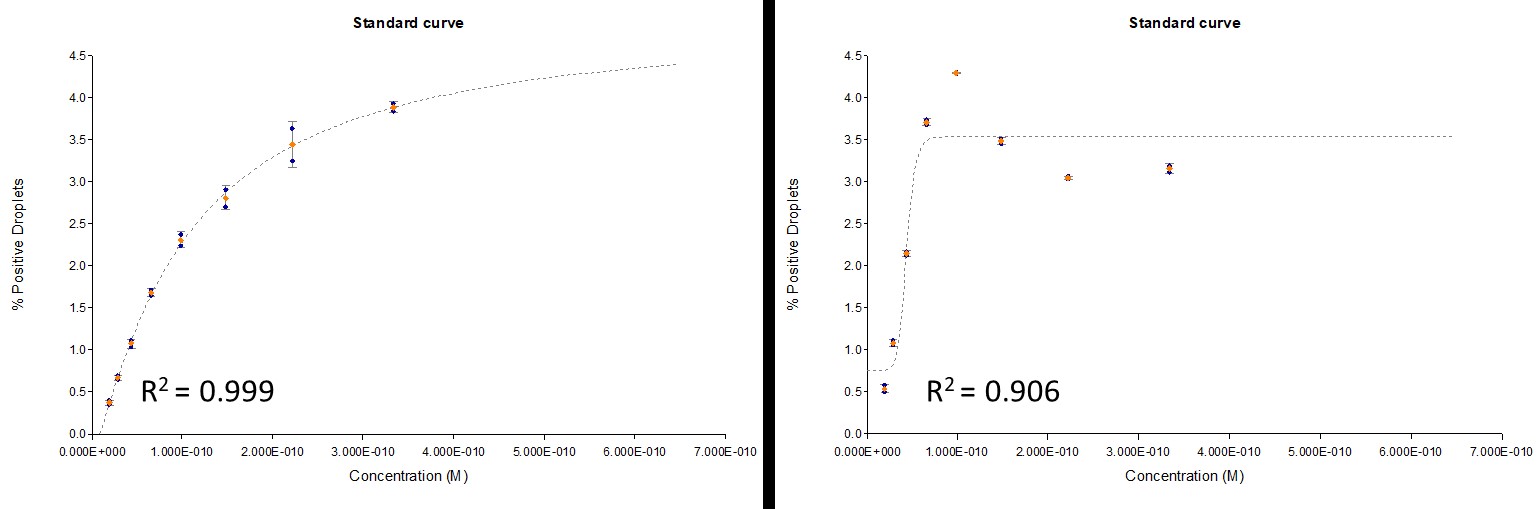Figure 2. The extension of the miRNA template is an inefficient process, resulting in inconsistent results in ddPCR. Examples of Standard curves generated from hybridization-based miRNA extension and ddPCR amplification. A 4-Parameter Logistic (4PL) non-linear regression was used for analysis, y = (A-D)/(1+(X/C)^B) + D. These exemplify the non-reliability of this Hybridization/Ligation and amplification approach due to the inconsistency of the template extension.

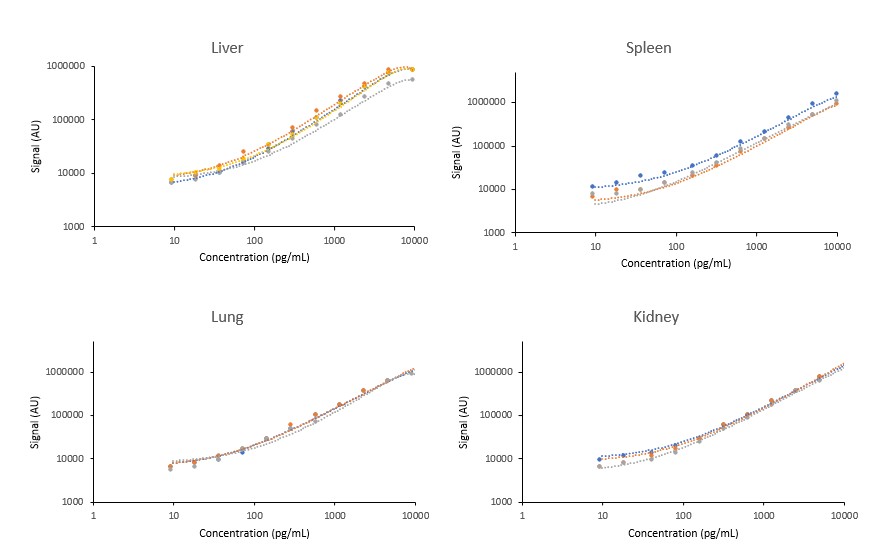Figure 3. Hybridization ECLIA is an effective method for bioanalysis and biodistribution analysis of microRNAs. Representative standard curves of spiked miRNA-122 template in homogenized Lung, Spleen, Lung, and Kidney. Each curve corresponds to an independent experiment and was traced using a 5-Parameter Logistic (5PL) non-linear regression, y = (A-D)/(1+eB(log(x)-C))E + D.