(T1530-03-17) Lattice Based Model to Study Drug Diffusion through Excipient Matrix

Purpose: Pharmaceutical Drug Delivery System are systems which deliver a drug into the body. A drug delivery system consists of a drug and an excipient. Polymeric excipients are usually employed in controlled release formulations to control the duration and rate of drug release. The various mass transport mechanisms involved in drug release are diffusion, dissolution, swelling, and erosion. Our work aims to model the drug release phenomena from a drug delivery system where diffusion is the governing release mechanism. Mechanistic modeling via mathematical equations is challenging due to the complexity of drug release phenomena, and the solutions obtained are intractable for practical use. Empirical models such as the Higuchi Law, Power Law, and Weibull function, although simple to use, are not exactly based on the actual description of the physical processes involved and thus cannot reliably predict release profiles for new formulations. To deal with these challenges, Monte Carlo (MC) techniques have been utilized to simulate various complex systems. It is based on the idea that drug release is often based on random fluctuations, making stochastic models a well-suited choice. MC simulation, although simplified, takes structural information into account and thus is a direct representation of the drug release phenomena. More accurate Molecular Dynamics (MD) simulations can effectively capture the underlying physics well, but are molecule-specific and thus results cannot be extended to other systems. MD simulations are also constrained by the time and length scales they can represent. Consequently, many studies, including ours, have modeled the diffusion process using MC simulations.

Methods: We consider Mesoscale Lattice-based models to study diffusion-driven drug release phenomena from the polymer matrix. The core idea is that the drug particles are essentially performing a two-dimensional “random walk” inside the polymer matrix. Thus, for the sake of simplicity, our model uses the analogy of ants performing a random walk on a maze, where the ants and maze represent the drug and excipient molecules, respectively. The lattice consists of two layers: a hydrophobic layer where ants (drug particles) form aggregates or crystals if they are present in adjacent cells and thus move together, and a hydrophilic layer where they do not. At the start of the simulation, all ants are initialized in the hydrophobic layer. The diffusion process is simulated by selecting an ant or ant aggregate at random and allowing it to move to an adjacent cell in any of the four directions, which is decided based on a random number generation process. Ants move inside the matrix with excluded volume interactions, meaning each ant occupies only one lattice site (cell) at a time that is not occupied by another ant. Movement of an ant to a cell already containing another ant is rejected. Polymeric excipients are present as walls (cell boundaries) between the cells, restricting the free movement of ants by randomly rejecting the attempts of ants to move to an adjacent cell. In one MC step, all ants and ant aggregates are allowed to move only once. An ant “escapes” the lattice when it moves out of the lattice from one of the boundary cells. Periodic boundary conditions are present in the horizontal direction to simulate bulk diffusion, while reflective boundary conditions at the bottom ensure that no ant can escape from the bottom of the lattice. A number of physically relevant and controllable parameters in our simulation, such as the size of the lattice (number of cells), number of MC steps, polymer loading (wall fraction), drug loading (ant fraction), excipient-drug interactions (probability of crossing wall), thickness of the hydrophobic and hydrophilic layers, are varied to provide results and to study the release profile, size distribution of ant aggregates formed due to trapping, and concentration of ants along the release direction at different timesteps.

Results: We analyze the effect of the various parameters on the release profile: Data from the simulation in the table indicates that an increase in wall fraction in the hydrophobic layer is mainly responsible for ant aggregates getting “trapped” (unreleased drug) in the matrix. The wall fraction in the hydrophilic layer has a negligible effect on the release of drug particles. The release profile in the image compares two cases with different hydrophobic layer thicknesses, revealing smaller values of hydrophobic layer thickness showing a more sustained release and reduced amount of unreleased drug.

Conclusion: The lattice-based model provides us with a qualitative understanding of the diffusion-driven release phenomena, which we will prove useful in designing controlled release formulations. It considers the impact of physically meaningful parameters on drug release. Future work would entail including the effects of other release mechanisms such as dissolution, erosion, and swelling of the matrix in the simulation.

References: Kosmidis K, Dassios G. Monte Carlo simulations in drug release. J Pharmacokinet Pharmacodyn. 2019 Apr;46(2):165-172. doi: 10.1007/s10928-019-09625-8. Epub 2019 Mar 18. PMID: 30880356.
Kosmidis K, Argyrakis P, Macheras P (2003b) A reappraisal of drug release laws using monte carlo simulations: the prevalence of the weibull function. Pharm Res 20(7):988–995
Singh, K., Satapathi, S. & Jha, P. K. “Ant-wall” model to study drug release from excipient matrix. Physica A: Statistical Mechanics and its Applications 519, 98 – 108 (2019)

Acknowledgements: The authors thank the financial support of Anusandhan National Research Foundation, India, project number CRG/2022/003774. The authors also gratefully acknowledge the facilities provided by the Indian Institute of Technology Roorkee.


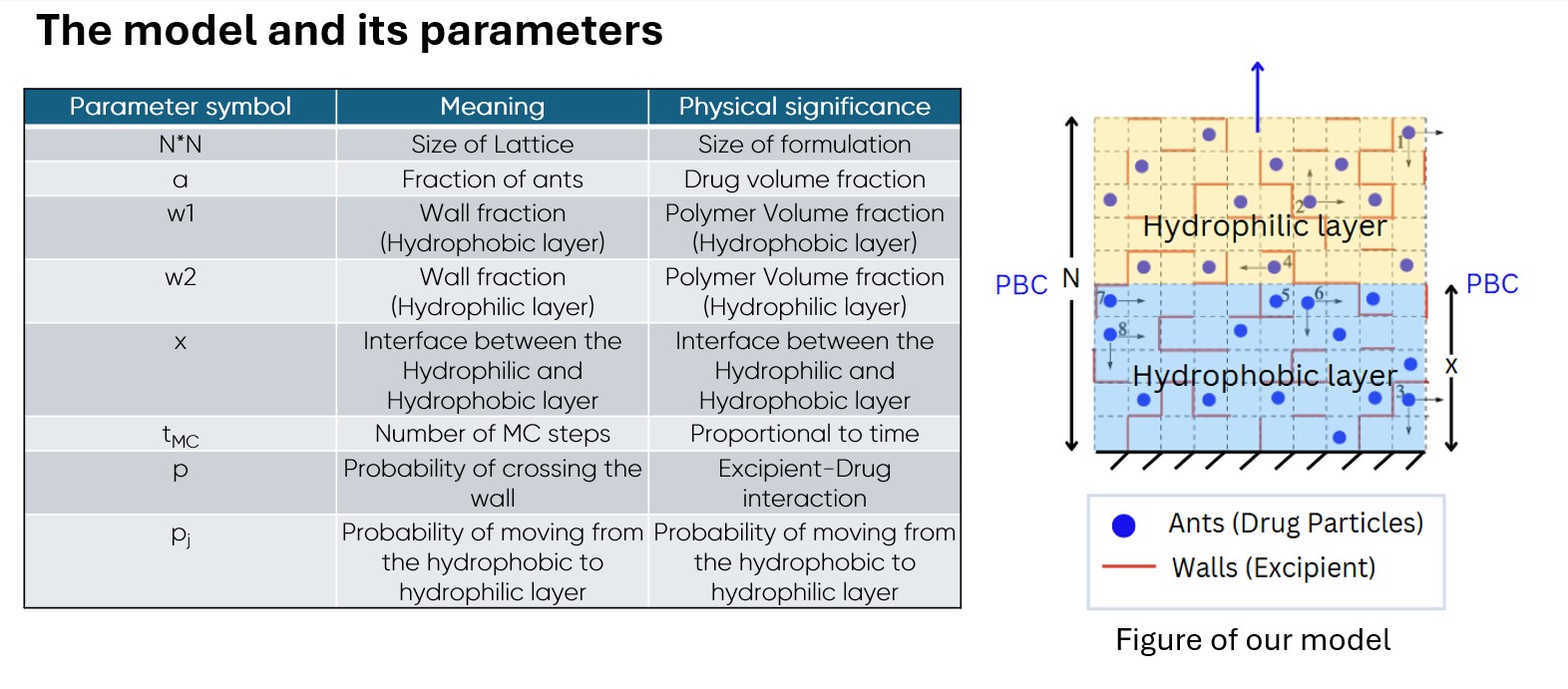
Schematic of the model


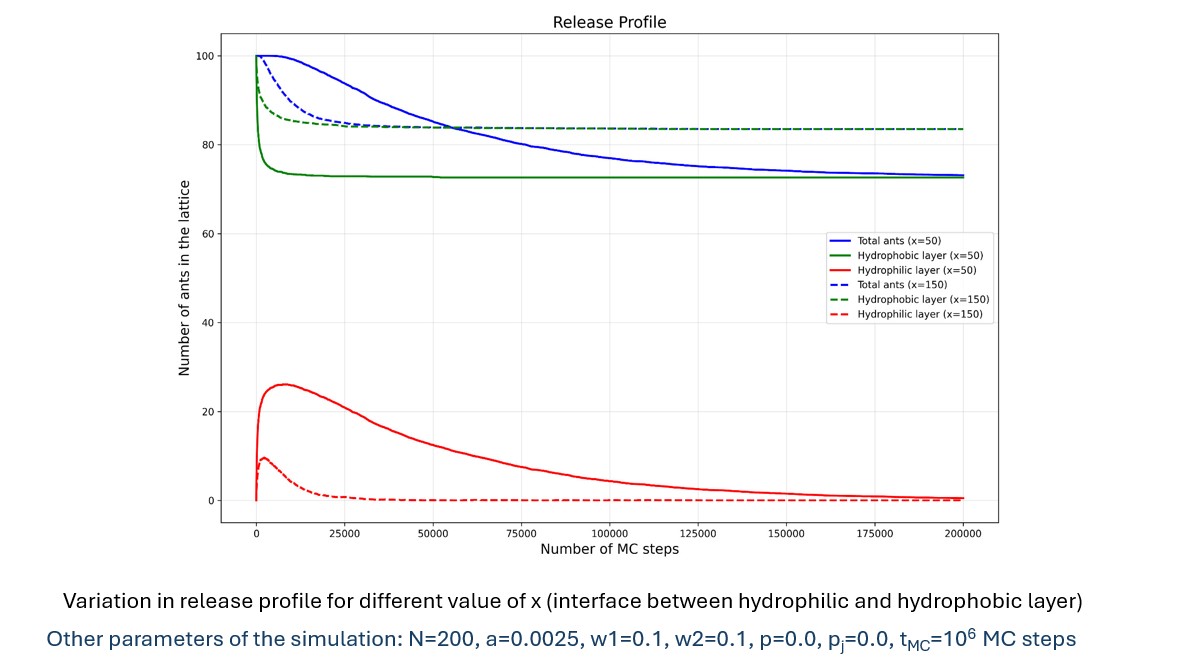
Drug Release Profile


Trapping of drug particles